3-22
k Differential Calculations [OPTN]-[CALC]-[d/dx]
To perform differential calculations, first display the function analysis menu, and then input the
values using the syntax below.
K4(CALC)2(
d/dx) f(x),a,tol!/( ) )
(
a: point for which you want to determine the derivative, tol: tolerance)
The differentiation for this type of calculation is defined as:
In this definition, infinitesimal is replaced by a sufficiently small A
x, with the value in the
neighborhood of f
'
(a) calculated as:
In order to provide the best precision possible, this unit employs central difference to perform
differential calculations.
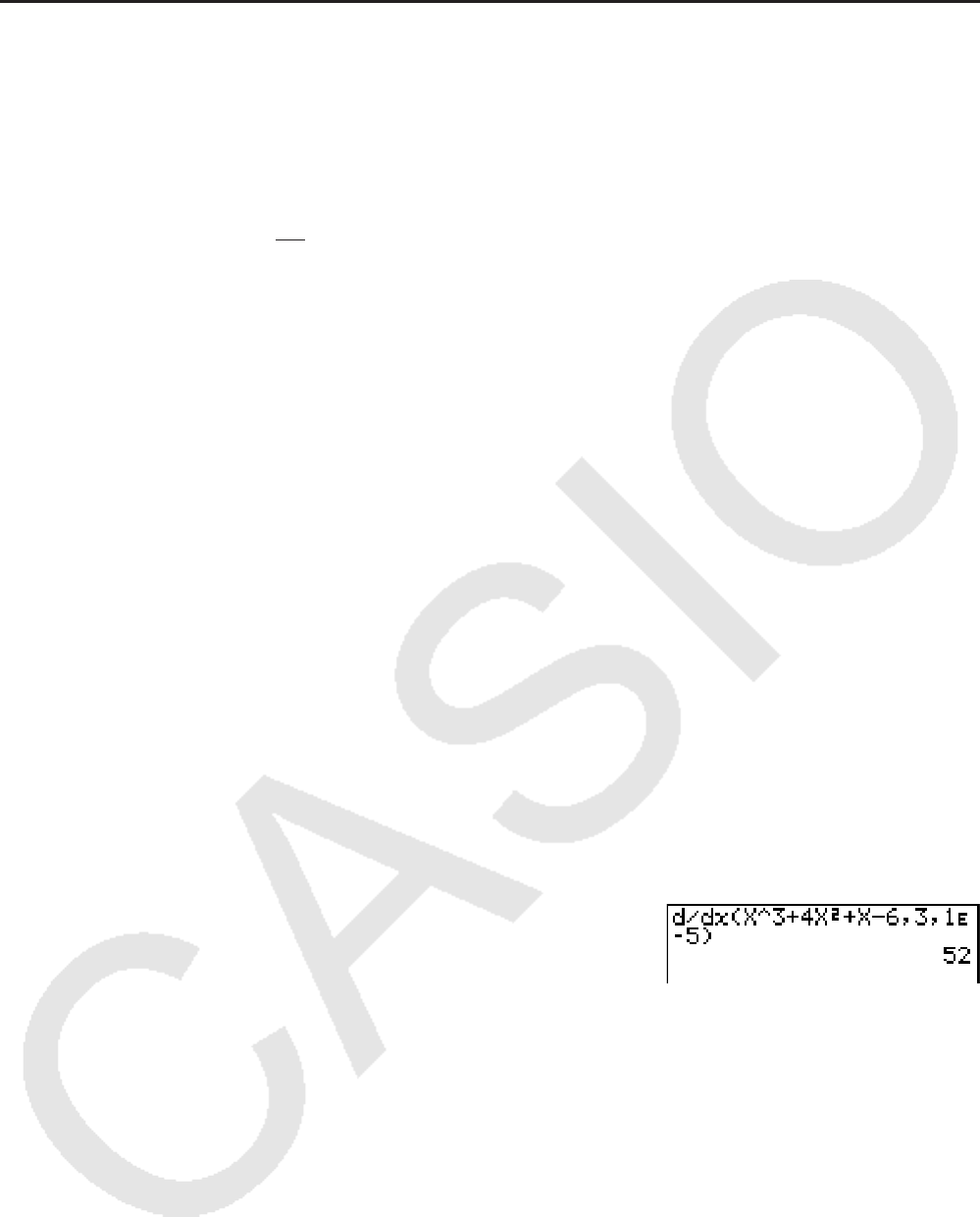
Example To determine the derivative at point
x = 3 for the function
y = x
3
+ 4 x
2
+ x – 6, with a tolerance of “ tol” = 1 E – 5
Input the function
f(x).
AK4(CALC)2(
d/dx)a5(U-Z)4(X)!a(CATALOG)
a6(SYBL)4(9)c~c(^)wd+ea5(U-Z)4(X)
x+4(X)-g,
Input point
x = a for which you want to determine the derivative.
d,
Input the tolerance value.
b!a(CATALOG)a1(A-E)5(E)
c~c(EXP)w-f!/( ) )w
Differential Calculation Precautions
• In the function f(x), only X can be used as a variable in expressions. Other variables
(A through Z excluding X,
r, Ƨ) are treated as constants, and the value currently assigned to
that variable is applied during the calculation.
• Input of the tolerance (
tol) value and the closing parenthesis can be omitted. If you omit
tolerance ( tol) value, the calculator automatically uses a value for tol as 1 E–10.
• Specify a tolerance (
tol) value of 1 E–14 or greater. An error (Time Out) occurs whenever no
solution that satisfies the tolerance value can be obtained.
• Pressing A during calculation of a differential (while the cursor is not shown on the display)
interrupts the calculation.
• Inaccurate results and errors can be caused by the following:
- discontinuous points in
x values
- extreme changes in
x values
- inclusion of the local maximum point and local minimum point in
x values
d
/
dx
(
f
(
x
)
a
)
⇒
f
(
a
)
dx
d
d
/
dx
(
f
(
x
)
a
)
⇒
f
(
a
)
dx
d
f
(
a
+
A
x
)–
f
(
a
)
f
(
a
) = lim
–––––––––––––
A
x
A
x
→
0
'
f
(
a
+
A
x
)–
f
(
a
)
f
(
a
) = lim
–––––––––––––
A
x
A
x
→
0
'
f
(
a
+
A
x
)–
f
(
a
)
f
(
a
)
–––––––––––––
A
x
'
Լ
f
(
a
+
A
x
)–
f
(
a
)
f
(
a
)
–––––––––––––
A
x
'
Լ
