ANALYTICAL METHODS FOR TEXTILE COMPOSITES
obtains normal to the applied load. From energy considerations, the isostress result, Eq.
(5.22b), always provides a lower bound to the stiffness; the isostrain result, Eq. (5.22a),
an upper bound.
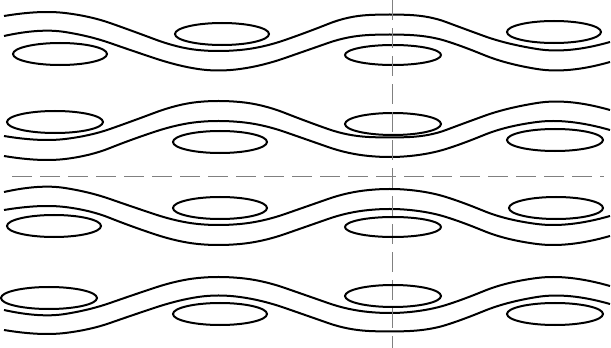
Figure 5-8. Three orthogonal symmetry planes (two marked by dashed lines and the
third being the plane of the figure) in a stack of woven plies, implying orthotropy
over gauge lengths that are larger than the ply thickness and the period of the weave.
Good design in airframes, which must be very stiff, requires positioning as many
straight fibers as possible in the directions of the largest anticipated stresses. Isostrain
conditions are then by far the better approximation.
In a 2D laminate, orientation averaging with isostrain conditions is equivalent to
standard laminate theory for in-plane deformations. Thus orientation averaging models
and models in which a textile is approximated geometrically as a laminate will yield
similar results for quasi-laminar textiles [5.8,5.22].
5.1.8 Bending or Axial Shear?
The response of a curved tow element to lateral loads is sometimes modeled as
that of a simple beam that can bend but not shear. The beam may be anchored at points
where the locus of the tow has extrema, usually at points where it is impinged upon by
other tows (perhaps at the boundary of a unit cell). However, this modeling approach is
valid only if the beam represents a tow segment whose length, L, is many multiples of its
thickness, 2t. If the tow segment is short, the primary contribution to its lateral deflection
will be axial shear deformation, not bending.
