PREDICTION OF ELASTIC CONSTANTS AND THERMAL EXPANSION
plane of mirror symmetry in the textile allows the use of a reduced cell in calculations,
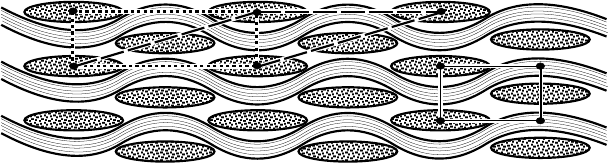
halving the size of the problem that has to be solved (solid line rectangle in Fig. 5-3).
Figure 5-3. Alternative unit cells (short and long dash lines at upper left) in a plane
woven laminate. The smaller, solid-lined rectangle (lower right) shows a reduced cell
that takes advantage of reflection symmetry about a vertical plane.
The interior of the unit cell is often modeled in fine detail. In typical unit cell
calculations, grids are defined to replicate each tow segment bounded by the cell and
each resin pocket between tows. Interior stresses and strains are computed by a finite
element simulation subject to periodic boundary conditions on the cell walls. Since the
unit cell is a 3D structure with heterogeneous and highly anisotropic components, even a
mildly complex textile architecture requires a large number of interior elements. Unit cell
calculations are usually computationally intensive. The output of unit cell calculations
includes both the spatially averaged response of the cell and details of stress distributions
among tows and resin pockets.
Some workers have minimized computational cost by introducing simplified
models of tow segments within the unit cell. For example, tow segments can be
represented crudely as bending or shearing beams; or the unit cell of a quasi-laminar
textile can be modeled by a variant of laminate theory. The properties of the unit cell are
then computed relatively easily. However, the quality of calculations of the details of
interior stress distributions is impaired.
When external loads are nonuniform, periodicity no longer exists in stresses and
strains; and periodic boundary conditions are no longer correct for the unit cell. The
strain in one cell of the composite has no simple relation to the strain in any of its
neighbors (Fig. 5-4). One approach to modeling such cases is to calculate and store the
response of a unit cell to uniform strains and uniform strain gradients; and then compute
the response of an assembly of such cells when the strains and strain gradients are
constrained to be compatible. In other words, the averaged response of the unit cell is
