PREDICTION OF ELASTIC CONSTANTS AND THERMAL EXPANSION
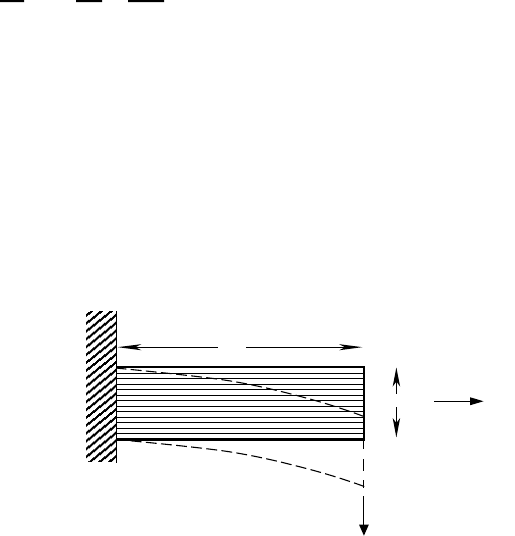
Fig. 5-9 shows a simple paradigm for estimating the relative importance of
bending and shear in a tow that is subject to lateral loads. Elementary calculations show
that the bending and shear deflections, v
b
and v
s
, are in the proportion
. (5.27)
where E
x
and G
xy
are the axial and shear moduli of the tow and
χ
is a geometrical factor
of order unity. For carbon/epoxy, for example, E
x
/G
xy
≈ 40 [5.23]. Shear will dominate
deflections for tow segments of aspect ratio less than 5; and in this case simple bending
beam models should not be used. Simple bending beam models may be appropriate for
satin weaves with long float or braids with flat tows, but they are inappropriate for plain
weaves or 3D interlock weaves [5.23].
Figure 5-9. A simple paradigm for estimating the contributions of shear and bending
to the deflection of a tow.
Axial shear deflections (i.e., shear deflections in a plane containing the beam axis)
are admitted in thick beam models, which incorporate rotational as well as bending
degrees of freedom. However, to date thick beam models have not been applied to
textiles.
Segments of tows are also sometimes represented as simple beams supported
continuously by an elastic foundation, rather than anchored at discrete points. This can be
a useful method of modeling delamination (loss of the foundation) and its effect in
buckling during axial compression. The foundation may also represent the constraining
effects of through-thickness reinforcement, in which case it will usually be much stiffer
and may be modeled as discrete rather than continuous (Fig. 5-10). However, the
foundation does not have the same effect as internal shear and therefore a similar
restriction of validity to long tow segments must apply. For many 3D composites,
including 3D weaves and braids, this means that a simple beam model will be useful only
