ANALYTICAL METHODS FOR TEXTILE COMPOSITES
over gauge lengths that are different integral multiples of the unit cell width must give
equal results. Measurements over nonintegral multiples of the cell width will show gauge
length dependence, but the variations will fall inversely with the number of unit cells
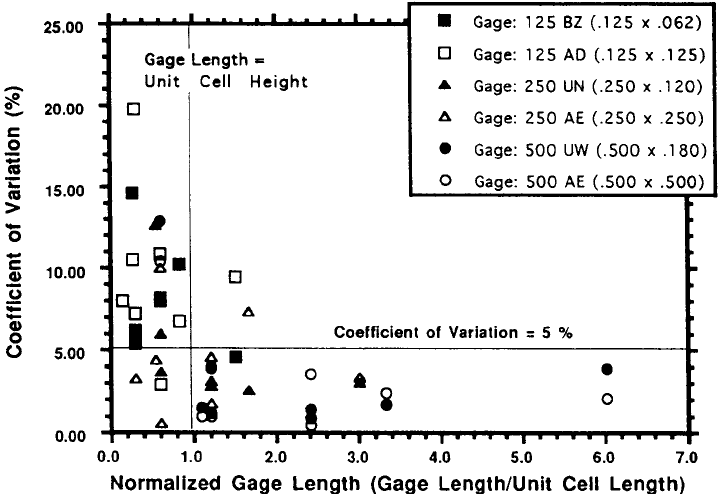
spanned by the gauge. In 2D braids, for example, variations in elastic modulus are a few
percent at most if the gauge length exceeds three unit cell widths (Fig. 5-6). But this
definition of
λ
i
can also be an unnecessarily conservative rule. If the textile architecture is
very complex, the unit cell will be large (e.g., Fig. 5-5). Yet large unit cells are often
divisible into subunits whose elasticity is similar but not identical; then homogeneity may
exist to a satisfactory degree over gauge lengths comparable to the subunits. Since the
degree to which subunits differ is continuously variable in many textile processes, no
general rule of thumb is possible.
Figure 5-6. Coefficient of variation of Young's modulus measurements as a function
of the size of the gauge used relative to the unit cell dimension in that direction (from
[5.12]). Gauge sizes shown in inches in inset; 1 in. ≈ 25.4 mm.
Rather than being periodic, i.e. invariant under certain nonzero translations, a 2D
laminate is invariant under translations of any size. It could be regarded as having a unit
cell of vanishing size in the in-plane directions. Applying the definition of
λ
i
suggested
for periodic textiles, a 2D laminate therefore may be considered to be homogeneous in
the in-plane directions over length scales that are vanishingly small. Similarly, a quasi-
laminar textile, which may have a large unit cell on geometrical considerations alone,
may be assigned vanishing values of
λ
i
for in-plane directions if it is sufficiently
