ANALYTICAL METHODS FOR TEXTILE COMPOSITES
σ
(o)
can be arbitrarily small for sufficiently severe flaws or damage. The maximum in-plane
stress for which the part can be designed falls commensurately.
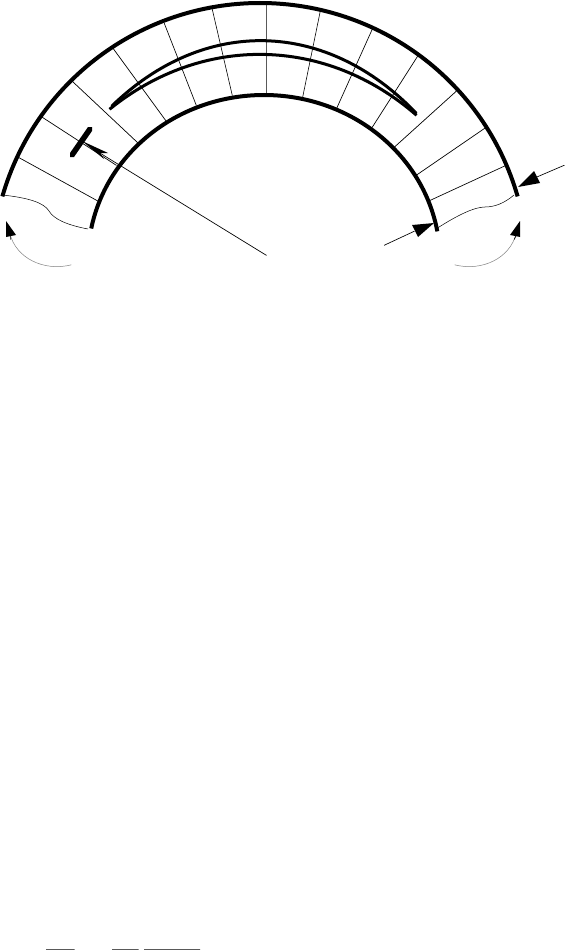
Figure 4-8. Stitching bridging a delamination crack in a curved part.
Through-thickness reinforcement such as stitching bridges delamination cracks,
shields the crack tip from the applied load, and thus can suppress delamination crack
growth. A simple, conservative bound to the effect of the stitches can be found by
considering them to be linear springs of length equal to the panel thickness [4.28]. For
such bridging springs, the critical stress for crack growth approaches a constant value,
σ
1
,
independent of crack length for sufficiently long delaminations [4.28,4.29]. The stress,
σ
1
,
can be related analytically to the properties of the stitches. Since
σ
1
is a lower bound to the
critical value of
σ
o
, a design rule can be deduced for the minimum volume fraction of
stitching fibers required to suppress delamination crack growth. One way of expressing the
rule is to require that
σ
o
<
σ
1
as long as
σ
(o)
<
σ
c
, where
σ
c
is the critical stress for in-plane
failure. If delamination is suppressed, the latter will probably be via kink band formation.
Then the volume fraction, f
s
, of stitching fibers must satisfy [4.28]
f
s
>
η
2
4
σ
c
2
h
2
r
m
2
h
E
s
G
Ic
(4.4)
where E
s
is the modulus of the stitching fibers and G
Ic
is the critical Mode I strain energy
release rate for a delamination crack in an unstitched laminate.
