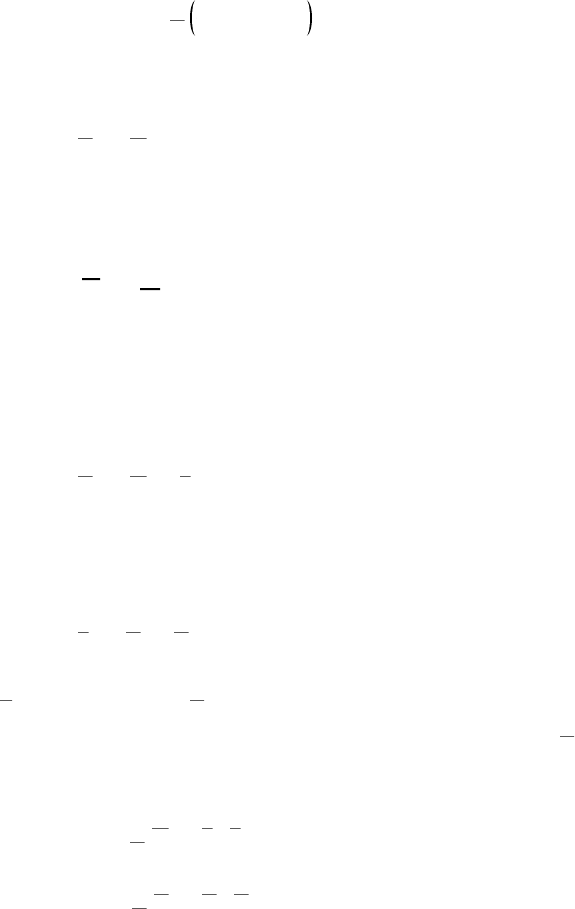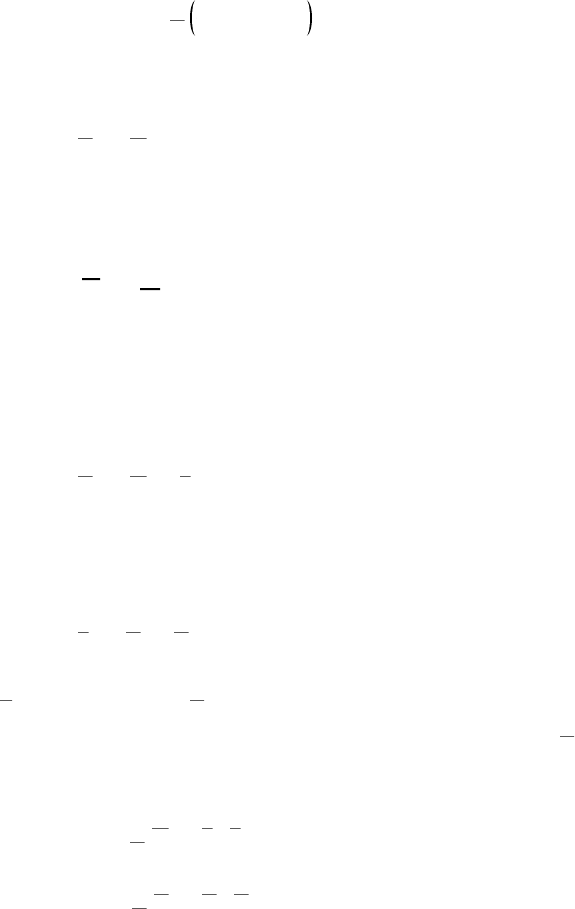
PREDICTION OF ELASTIC CONSTANTS AND THERMAL EXPANSION
Then the stress at any point is given by
σ
ij
(x) =
ε
kl
0
C
ijmn
(x)
ε
mn
(kl)
(x)
(5.15)
where
ε
ij
(kl)
(x) =
1
2
u
i,j
(kl)
+ u
j,i
(kl)
. (5.16)
Taking a volume average of Eq. (5.15) gives
(5.17)
where
C
V
C x x dV
ijkl ijmn mn
kl
=
1
( ) ( )
( )
ε
(5.18)
(If the strain multipliers
are uniform and of value unity, then Eq. (5.18) reduces to
the volume averaging of stiffness. This is the isostrain case.) From the average strain
theorem, Eq. (5.5), Eq. (5.17) can be written as
, (5.19)
By a similar derivation, if an elastic body is subject to the homogeneous tractions of Eq.
(5.12), then
. (5.20)
where
is the inverse of
. Assuming homogeneous boundary conditions of either Eq.
(5.10) or Eq. (5.12), it can be shown from the definition of
that strain and stress
energies are given respectively by
. (5.21)
Thus there is an exact correspondence between volume averaging and the definition of
effective macroscopic properties based on energy expressions [5.14].